Contents:
- Introduction
- Basic Building Blocks of Classical Sampling Theory
- Types of Sampling
- Sampling Distribution: Overview
- Conclusion
1. Introduction:
Predictive models are developed over a specific time period and on a certain set of records. However, implementation happens on a mutually exclusive time period (Out of Time Sample). Therefore, the models developed need to be trained and validated on different datasets: 1. Model Development Data (training data) 2. In sample validation data 3. Out of time validation data. A predictive model is considered to be robust, if their performance remains more or less stable in the out of time samples. An important observation from the description above is the following: The entire data (Population) is never accessible for model development and hence, is unknown. Models are developed on subsets (Samples) which are representative of the entire data. Representativeness of the samples are important to ensure the robustness in the model performance. This blog explores the key concepts related to creating representative samples from the population. Section 2 describes the basic components of the classical sampling theory, Section 3 describes the key types of sampling, Section 4 introduces the concept of Sampling Distribution and Section 5 concludes with the key summary of findings.
2. Basic Building Blocks of Classical Sampling Theory:
Introduction To Population and Sample
The two basic blocks of Classical Sampling Theory are: 1. Population 2. Samples. Populationis defined as the base of all the observations which are eligible to be studied to address key questions relating to a statistical investigation or a business problem, irrespective of whether it can be accessed or not. In real time the entire population is always unknown since there is a part of the population which cannot be accessed due to different reasons such as: Data Archiving Problems, Data permissions, Data Accessibility etc. A representative subset of the population is called a sample. The distribution of the variables in the sample is used to form an idea about the respective distribution of the variables in the population.
In a real time, any predictive modelling exercise uses the samples, since they cannot practically use the population. The population is not accessible because of the following reasons:
- Observation Exclusions used in models: Observation Exclusions are used in predictive models to remove unnecessary observations, which are redundant for analysis. For example, when developing a credit risk model, observations which are bankrupts or frauds are removed from the analysis, since frauds and bankrupts are a part of operational risk.
- Variable Exclusions used in the models: Variable Exclusions are used in predictive models to remove unnecessary variables which are redundant for analysis. For example, when developing a credit risk model, variables which are market-oriented variables or operational variables are excluded.
- Robustness Check of the developed models: The developed models are validated on multiple samples such as In-sample Validation data, Out of Time Validation samples Therefore, only a fraction of the dataset is available for model development. Hence, the population is always unknown, irrespective of the datasets, and hence the key statistical distributions of the population are anonymous
Mathematical Framework To Describe The Sampling Theory Framework:
Let X be a N x k vector (where N = Total number of rows that the matrix has (observation) and k = Total number of columns (variables)) which is normally distributed with mean μ and variance ![]() The population mean μ and variance both are unknown numerical features of the population distribution. These are called the Parameters: A functional form of all the population observations.
The population mean μ and variance both are unknown numerical features of the population distribution. These are called the Parameters: A functional form of all the population observations.
The key objective of the Classical Sampling Theory is to provide the appropriate guidelines for analysing the Population parameters based on the statistical moments of the sample. The statistical moments of the samples are called Estimators. The Estimators are a functional form of all the sample observations. For example, let us assume a subset of size ‘n’ is extracted from X such that the sample S is a n x k vector which is normally distributed.![]() are the sample means and the sample variance respectively. The descriptive moments are called statistics. A Statistic is an estimator with a sampling distribution. (Detailed Discussion: Section 4). The key objective of the classical sampling theory is to estimate the population parameters using the sample statistics, such that any difference between the two measures are statistically insignificant and considered to be an outcome of sampling fluctuations.
are the sample means and the sample variance respectively. The descriptive moments are called statistics. A Statistic is an estimator with a sampling distribution. (Detailed Discussion: Section 4). The key objective of the classical sampling theory is to estimate the population parameters using the sample statistics, such that any difference between the two measures are statistically insignificant and considered to be an outcome of sampling fluctuations.
Classical Sampling Methods:
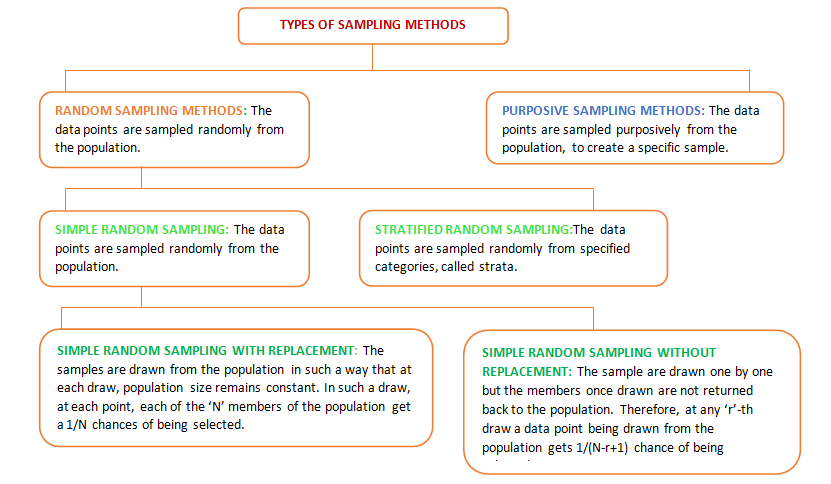
3. Types of Sampling
Broadly, there are two types of sampling methods discussed under the Classical Sampling theory: (i) Random Sampling (ii) Purposive Sampling. The different types of sampling and a brief description of each is provided in the figure below:
Applications Of Sampling Methods:
In the real time predictive modelling exercise, Stratified Random Sampling is considered to be of a wider appeal, than the Simple Random Sampling. Business datasets contain different categorical variables like: Product Type, Branch Size category, Gender, Income Groups etc. While splitting the total data into development data and Validation data, it is important to ensure that representation of the key categorical variables is made in the samples. This is important to ensure representativeness of the sample and robustness of the model. In this case a stratified random sampling is more preferred than the Simple Random Sampling. The use of Simple Random Sampling is limited to the cases where the data is symmetric and not much of heterogeneity is observed among the distribution of the values of the variables. The following examples discuss the applications of the Classical Sampling methods:
Example01: Splitting the Model Development Data into Training and Validation dataset
Models, when developed needs to be validated. The standard practice is to divide the data into 70% – 30% proportion. The models are trained on 70% of the observations and validated using the remaining 30%. To ensure the robustness of the model the distribution of the target variable should be similar in both the development and validation datasets. Therefore, the target variable is used as the Strata variable.
Example02: Boot Strapping Analysis
Boot Strapping Exercises exhaustively use Simple Random Sampling with Replacement. It is a nonparametric resampling method used to assign measures of accuracy to sample estimates.

4. Sampling Distribution: Overview
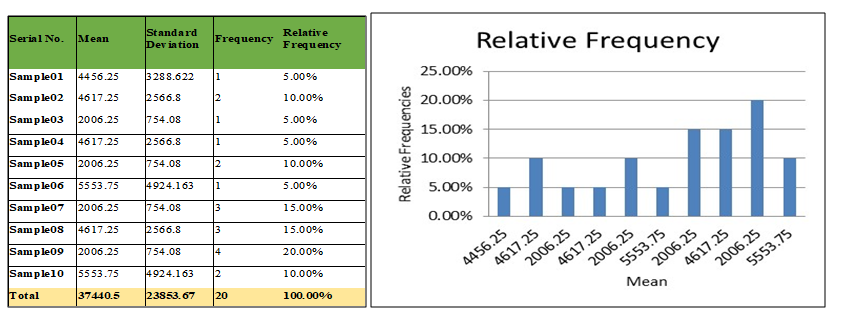
Sampling distribution of a statistic may be defined as the probability law which the statistic follows, if repeated random samples of a fixed size are drawn from specified population. A number of samples, each of size n, are taken from the same population and if for each sample the values of the statistic is calculated, a series of values of the statistic will be obtained. If the number of samples is large, these may be arranged into a frequency table. The frequency distribution of the statistic that would be obtained if the number of samples, each of the same size (say n), were infinite is called the Sampling distribution of the statistic. The table below shows a Sample Distribution and its associated frequency distribution:
5. Conclusion:
The blog, brought to you by DexLab Analytics, a premier institute conducting statistical analytics courses in Gurgaon and business analysis training in Delhi, introduces the basic concepts of Classical Sampling Framework. The objective here has been to explore the broad tenets of sampling theory, such as the different methods of sampling, their usages and their respective advantages and disadvantages. The Stratification Random Sampling is a more versatile sampling method compared to Simple Random Sampling methods. The concept of Sampling Distribution has been introduced but not discussed in details. This is to be the subject matter of the next blog: Sampling Distributions and its importance in Sampling theory.
Akash Dasgupta
Research Associate, DexLab Analytics
.