data analyst institute Archives - Page 3 of 11 - DexLab Analytics | Big Data Hadoop SAS R Analytics Predictive Modeling & Excel VBA

Category: data analyst institute

Bayes’ Theorem: A Brief Explanation

Posted on by Dexlab

Bayes’ Theorem: A Brief Explanation

(This is in continuation of the previous blog, which was published on 22nd April, 2019 – www.dexlabanalytics.com/blog/a-beginners-guide-to-learning-data-science-fundamentals )

In this blog, we’ll try to get a hands-on understanding of the Bayes’ Theorem. While doing so, hopefully we’ll be able to grasp a basic understanding of concepts such as Prior odds ratio, Likelihood ratio and Posterior odds ratio.

Arguably, a lot of classification problems have their root in Bayes’ Theorem. Reverend T. Bayes came up with this superior logical function, which mathematically deducts the probability of an event occurring from a larger set by “flipping” the conditional probabilities.

 


 

Consider,  E1, E2, E3,……..En to be a partition a larger set “S” and now define an Event – A, such that A is a subset of S.

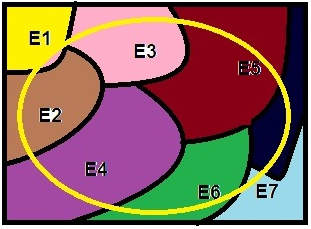
Let the square be the larger set “S” containing mutually exclusive events Ei’s.  Now, let the yellow ring passing through all Ei’s be an event – A.

Using conditional probabilities, we know,

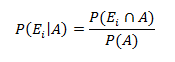
Also, the relationship: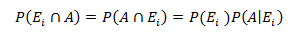

Law of total probability states: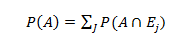

Rearranging the values of  &  gives us the Bayes Theorem: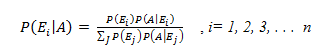

The values of  are also known as prior probabilities, the event A is some event, which is known to have occurred and the conditional probability   is known as the posterior probability.

Now that, you’ve got the maths behind it, it’s time to visualise its practical application. Bayesian thinking is a method of applying Bayes’ Theorem into a practical scenario to make sound judgements.

The next blog will be dedicated to Bayesian Thinking and its principles.

For now, imagine, there have been news headlines about builders snooping around houses they work in. You’ve got a builder in to work on something in your house. There is room for all sorts of bias to influence you into believing that the builder in your house is also an opportunistic thief.

However, if you were to apply Bayesian thinking, you can deduce that only a small fraction of the population are builders and of that population, a very tiny proportion is opportunistic thieves. Therefore, the probability of the builder in your house being an opportunistic thief is actually a product of the two proportions, which is indeed very-very small.

Technically speaking, we call the resulting posterior odds ratio as a product of prior odds ratio and likelihood ratio. More on applying Bayesian Thinking coming up in the next blog.

In the meantime try this exercise and leave your comments below in the comments section.

2

In the above example on “snooping builders”, what are your:

  • Ei’s
  • Event – A
  • “S”

About the Author: Nish Lau Bakshi is a professional data scientist with an actuarial background and a passion to use the power of statistics to tackle various pressing, daily life problems.

About the Institute: DexLab Analytics is a premier data analyst training institute in Gurgaon specializing in an enriching array of in-demand skill training courses for interested candidates. Skilled industry consultants craft state-of-the-art big data courses and excellent placement assistance ensures job guarantee.

For more from the tech series, stay tuned!

 

Interested in a career in Data Analyst?

To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.

To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.

General Python Guide 2019: Learning Data Analytics with Python

Posted on by Dexlab

General Python Guide 2019: Learning Data Analytics with Python

Python and data analytics are possibly three of the most commonly heard words these days. In today’s burgeoning tech scene, being skillful in these two subjects can prove very profitable. Over the years, we have seen the importance of Python education in the field of data science skyrocketing.

So here we present a general guide to help start off your Python learning:

Reasons to Choose Python:

  • Popularity

With over 40% data scientists preferring Python, it is clearly one of the most widely used tools in data analysis. It has risen in popularity above SAS and SQL, only lagging behind R.

  • General Purpose Language

There might be many other great tools in the market for analyzing data, like SAS and R, but Python is the only trustworthy general-purpose language valid across a number of application domains.

2

Step 1: Setup Python Environment

Setting up Python environment is uncomplicated, but a primary step. Downloading the free Anaconda Python package is recommended. Besides core Python language, it includes all the essential libraries, such as Pandas, SciPy, NumPy and IPython, and graphical installer also. Post installation, a package containing several programs is launched, most important one being iPython also known as Jupyter notebook. After launching the notebook, the terminal opens and a notebook is started in the browser. This browser works as the coding platform and there’s no need for internet connection even.

Step 2: Knowing Python Fundamentals

Getting familiar with the basics of Python can happen online. Active participation in free online courses, where video tutorials, practice exercises are plentiful, can help you grasp the fundamentals quickly. However, if you are seeking expert guidance, you must explore our Python data science courses.

Step 3: Know Key Python Packages used for Data Analysis

Since it is a general purpose language, Python’s utility stretches beyond data science. But there are plentiful Python libraries useful in data functionalities.

Numpy – essential for scientific computing

Matplotib – handy for visualization and plotting

Pandas – used in data operations

Skikit-learn – library meant to help with data mining and machine learning activities

StatsModels – applied for statistical analysis and modeling

Scipy-SciPy – the Numpy extension of Python; it is a set of math functions and algorithms

Theano – package defining multi-dimensional arrays.

Step 4: Load Sample Data for Practice

Working with sample datasets is a great way of getting familiar with a programming language. Through this kind of practice, candidates can try out different methods, apply novel techniques and also pinpoint areas of strength and in need of improvement.

Python library StatModels contains preloaded datasets for practice. Users can also download dataset from CSV files or other sources on web.

Step 5: Data Operations

Data administration is a key skill that helps extract information from raw data. Majority of times, we get access to crude data that cannot be analyzed straightaway; it needs to be manipulated before analyzing. Python has several tools for formatting, manipulating and cleaning data before it is examined.

Step 6: Efficient Data Visualization

Visuals are very valuable for investigative data analysis and also explaining results lucidly. The common Python library used for visualization is Matplotlib.

Step 7: Data Analytics

Formatting data and designing graphs and plots are important in data analysis. But the foundation of analytics is in statistical modeling, data mining and machine learning algorithms. Having libraries like StatsModels and Scikit-learn, Python provides all necessary tools essential for performing core analyzing functions.

Concluding

As mentioned before, the key to learning data analytics with Python is practicing with imported data sets. So without delay, start experimenting with old operations and new techniques on data sets.

For more useful blogs on data science, follow DexLab Analytics – we help you stay updated with all the latest happenings in the data world! Also, check our excellent Python courses in Delhi NCR.

 

Interested in a career in Data Analyst?

To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.

To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.

Being a Statistician Matters More, Here’s Why

Posted on by Dexlab

Being a Statistician Matters More, Here’s Why

Right data for the right analytics is the crux of the matter. Every data analyst looks for the right data set to bring value to his analytics journey. The best way to understand which data to pick is fact-finding and that is possible through data visualization, basic statistics and other techniques related to statistics and machine learning – and this is exactly where the role of statisticians comes into play. The skill and expertise of statisticians are of higher importance.

2

Below, we have mentioned the 3R’s that boosts the performance of statisticians:

Recognize – Data classification is performed using inferential statistics, descriptive and diverse other sampling techniques.

Ratify – It’s very important to approve your thought process and steer clear from acting on assumptions. To be a fine statistician, you should always indulge in consultations with business stakeholders and draw insights from them. Incorrect data decisions take its toll.

Reinforce – Remember, whenever you assess your data, there will be plenty of things to learn; at each level, you might discover a new approach to an existing problem. The key is to reinforce: consider learning something new and reinforcing it back to the data processing lifecycle sometime later. This kind of approach ensures transparency, fluency and builds a sustainable end-result.

Now, we will talk about the best statistical techniques that need to be applied for better data acknowledgment. This is to say the key to becoming a data analyst is through excelling the nuances of statistics and that is only possible when you possess the skills and expertise – and for that, we are here with some quick measures:

Distribution provides a quick classification view of values within a respective data set and helps us determine an outlier.

Central tendency is used to identify the correlation of each observation against a proposed central value. Mean, Median and Mode are top 3 means of finding that central value.

Dispersion is mostly measured through standard deviation because it offers the best scaled-down view of all the deviations, thus highly recommended.

Understanding and evaluating the data spread is the only way to determine the correlation and draw a conclusion out of the data. You would find different aspects to it when distributed into three equal sections, namely Quartile 1, Quartile 2 and Quartile 3, respectively. The difference between Q1 and Q3 is termed as the interquartile range.

While drawing a conclusion, we would like to say the nature of data holds crucial significance. It decides the course of your outcome. That’s why we suggest you gather and play with your data as long as you like for its going to influence the entire process of decision-making.

On that note, we hope the article has helped you understand the thumb-rule of becoming a good statistician and how you can improve your way of data selection. After all, data selection is the first stepping stone behind designing all machine learning models and solutions.

Saying that, if you are interested in learning machine learning course in Gurgaon, please check out DexLab Analytics. It is a premier data analyst training institute in the heart of Delhi offering state-of-the-art courses.

 

The blog has been sourced from — www.analyticsindiamag.com/are-you-a-better-statistician-than-a-data-analyst

 

Interested in a career in Data Analyst?

To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.

To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.

How Deep Learning is Solving Forecasting Challenges in Retail Industry

Posted on by Dexlab

How Deep Learning is Solving Forecasting Challenges in Retail Industry

Known to all, the present-day retail industry is obsessed with all-things-data. With Amazon leading the show, many retailers are found implementing a data-driven mindset throughout the organization. Accurate predictions are significant for retailers, and AI is good in churning out value from retail datasets. Better accuracy in forecasts has resulted in widespread positive impacts.

2

Below, we’ve chalked down how deep learning, a subset of machine learning addresses retail forecasting issues. It is a prime key to solve most common retail prediction challenges – and here is how:

  • Deep learning helps in developing advanced, customized forecasting models that are based on unstructured retail data sets. Relying on Graphic Processing Units, it helps process complex tasks – though GPUs area applied only twice during the process; once during training the model and then at the time of inference when the model is applied to new data sets.

  • Deep learning-inspired solutions help discover complex patterns in data sets. In case of big retailers, the impressive technology of Deep Learning supports multiple SKUs all at the same time, which proves productive on the part of models as they get to learn from the similarities and differences to seek correlations for promotion or competition. For example, winter gloves sell well when puffer jackets are already winning the market, indicating sales. On top of that, deep learning can also ascertain whether an item was not sold or was simply out of stock. It also possesses the ability to determine the larger problem as to why the product was not being sold or marketed.

  • For a ‘cold start’, historical data is limited but deep learning has the power to leverage other attributes and boost the forecasting. The technology works by picking similar SKUs and implement that information to bootstrap forecasting process.

Nonetheless, there exists an array of challenges associated with Deep Learning technology. The very development of high-end AI applications is at a nascent stage; it is yet to become a fully functional engineering practice.

A larger chunk of successful AI implementation depends on the expertise and experience of the breed of data scientists involved. Handpicking a qualified data scientist in today’s world is the real ordeal. Being fluent in the nuances of deep learning imposes extra challenges. Moreover, apart from being labor intensive in terms of feature engineering and data cleaning, the entire methodology of developing neural network models all manually is difficult and downright challenging. It may even take a substantial amount of time to learn the tricks and scrounge through numerous computational resources and experiments performed by data scientists. All this makes the hunt down for skilled data scientists even more difficult.

Fortunately, DexLab Analytics is here with its top of the line data science courses in Gurgaon. The courses offered by the prominent institute are intensive, well-crafted and entirely industry-relevant. For more information on data analyst course in Delhi NCR, visit our homepage.

 
The blog has been sourced from ―
www.forbes.com/sites/nvidia/2018/11/21/how-deep-learning-solves-retail-forecasting-challenges/#6cf36740db18
 

Interested in a career in Data Analyst?

To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.

To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.

Databricks Supports Apache Spark 2.4 and Adds ML Runtime

Posted on by Dexlab

Databricks Supports Apache Spark 2.4 and Adds ML Runtime

Databricks recently embraced the Apache Spark 2.4, a latest version. They are integrating it into their platform of analytics. Also, the company is on its way to unveil another runtime feature that would simplify the intricacies of deep learning.

Needless to say, Databricks is one of the most powerful supporters of version 2.4 of Spark, the notable stream processing framework.  The latest upgraded version features improvement in the performance of machine learning framework running on Spark as well as distributed deep learning. It also includes modifications that would instantly address dependency issues related to deep learning tasks.

Project Hydrogen is an ambitious initiative; it’s under this tag the Spark upgrades were fused and introduced as a new scheduling mode, known as ‘barrier execution’. It encourages developers to embed training in lieu of distributed deep learning posed as an Apache Spark workload.

In context to above, Reynold Xin, a staunch Spark contributor and co-founder at Databricks said, “This is the largest change to Spark’s scheduler since the inception of the project.” He further mentioned that the upgrades will actually help reduce the complexities of machine learning structures and ensure high efficacy.

The latest runtime detail categorized HorovodRunner is developed to rationalize scaling and streamlining of distributed deep learning workloads. It is performed from a single machine to huge clusters. Previously, drifting from single-node workloads to huge distributed training on GPU or CPU clusters needed a bunch of full code rewrites – it was exceedingly challenging enough. Undeniably, HorovodRunner reduces training as well as programming time cutting down them from hours to a few minutes. This was claimed by the professionals working at Databricks.

Besides Horovod, Databricks is found to be saying that its platform offers native integration with TensorFlow, Kera and several other machine learning programs coupled with MLib and GraphFrames super machine learning algorithms.

On top of all this, a few weeks back, Databricks associated itself with a versatile cloud data integrator Talend with a sole aim to integrate the cloud service with their own data analytics platform to allow data scientists leverage the cluster computing framework – it would help process large data sets at scale.

About Apache Spark:

Apache Spark is a robust, well-integrated analytics engine efficient in processing large datasets. Crafted for high speed, productivity and generic use, it is considered as one of the most popular projects in motion under Apache software umbrella. It is also one of the most volatile and active open source big data projects.

DexLab Analytics is a top-notch Apache Spark training institute in Gurgaon. It provides top of the line in-demand skill training on a plethora of new-age IT related courses, such as data science, data analytics courses, big data, risk analytics and more.

 

The blog was sourced from ― www.datanami.com/2018/11/19/databricks-upgrades-spark-support-adds-ml-runtime

 

Interested in a career in Data Analyst?

To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.

To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.

Private Banks, Followed by E-commerce and Telecom Industry Shows High Adoption Rates for Data Analytics

Posted on by Dexlab

Private Banks, Followed by E-commerce and Telecom Industry Shows High Adoption Rates for Data Analytics

Are you looking for a data analyst job? The chances of bagging a job at a private bank are more than that a public bank. The former is more likely to hire you than the latter.

As a matter of fact, data analytics is widely being used in the private banking and e-commerce sectors – according to a report on the state of data analytics in Indian business. The veritable report was released last month by Analytics India Magazine in association with the data science institute INSOFE. Next to banking and ecommerce, telecom and financial service sectors have started to adopt the tools of data analytics on a larger scale, the report mentioned.

The report was prepared focusing on 50 large firms across myriad sectors, namely Maruti Suzuki and Tata Motors in automobiles, ONGC and Reliance Industries under oil-drilling and refineries, Zomato and Paytm under e-commerce tab, and HDFC and the State Bank of India in banking.

2

If you follow the study closely, you will discover that in a nutshell, data analytics and data science boasts of a healthy adoption rate all throughout – 64% large Indian firms has started implementing this wonder tool at their workplaces. As a fact, if a firm is found to have an analytics penetration rate of minimum 0.75% (which means, at least one analytics professional is found out of 133 employees in a company), we can say the company has adopted analytics.

Nevertheless, the rate of adoption was not universal overall. We can see that infrastructure firms have zero adoption rates – this might be due to a lack of resources to power up a robust analytics facility or whatever. Also, steel, power and oil exhibited low adoption rates as well with not even 40% of the surveyed firms crossing the 0.75% bar. On contrary, private banks and telecom industry showed a total 100% adoption rates.

Astonishingly, public sector banks showed a 50% adoption rate- almost half of the rate in the private sector.

The study revealed more and more companies in India are looking forward to data analytics to boost sales and marketing initiatives. The tools of analytics are largely employed in the sales domain, followed by finance and operations.

Apparently, not much of the results were directly comparable with that of the last year’s study. Interestingly, one metric – analytics penetration rate – was measured last year as well, which is nothing but the ratio of analytics-oriented employees to the total. Also, last year, you would have found one out of 59 employees in an average organization, which has now reached one data analyst for every 36 employees.

For detailed information, read the full blog here: qz.com/india/1482919/banks-telcos-e-commerce-firms-hire-most-data-analysts-in-india

If you are interested in following more such interesting blogs and technology-related updates, follow DexLab Analytics, a premium analytics training institute headquartered in Gurgaon, Delhi. Grab a data analyst certification today and join the bandwagon of success.

 

Interested in a career in Data Analyst?

To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.

To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.

Data Driven Projects: 3 Questions That You Need to Know

Posted on by Dexlab

Data Driven Projects: 3 Questions That You Need to Know

Today, data is an asset. It’s a prized possession for companies – it helps derive crucial insights about customers, thus future business operations. It also boosts sales, predicts product development and optimizes delivery chains.

Nevertheless, several recent reports suggest that even though data floats around in abundance, a bulk of data-driven projects fail. In 2017 alone, Gartner highlighted 60% of big data projects fail – so what leads it? Why the availability of data still can’t ensure success of these projects?

2

Right data, do I have it?

It’s best to assume the data which you have is accurate. After all, organizations have been keeping data for years, and now it’s about time they start making sense out of it. The challenge that they come across is that this data might give crucial insights about past operations, but for present scenario, they might not be good enough.

To predict the future outcomes, you need fresh, real-time data. But do you know how to find it? This question leads us to the next sub-head.

Where to find relevant data?

Each and every company does have a database. In fact, many companies have built in data warehouses, which can be transformed into data lakes. With such vast data storehouses, finding data is no more a difficult task, or is it?

Gartner report shared, “Many of these companies have built these data lakes and stored a lot of data in them. But if you ask the companies how successful are you doing predictions on the data lake, you’re going to find lots and lots of struggle they’re having.”

Put simply, too many data storehouses may pose a challenge at times. The approach, ‘one destination for all data in the enterprise’ can be detrimental. Therefore, it’s necessary to look for data outside the data warehouses; third party sources can be helpful or even company’s partner network.

How to combine data together?

Siloed data can be calamitous. Unsurprisingly, data is available in all shapes and is derived from numerous sources – software applications, mobile phones, IoT sensors, social media platforms and lot more – compiling all the data sources and reconciling data to derive meaningful insights can thus be extremely difficult.

However, the problem isn’t about the lack of technology. A wide array of tools and software applications are available in the market that can speed up the process of data integration. The real challenge lies in understanding the crucial role of data integration. After all, funding an AI project is no big deal – but securing a budget to address the problem of data integration efficiently is a real challenge.

In a nutshell, however data sounds all promising, many organizations still don’t know how achieve full potential out of data analytics. They need to strengthen their data foundation, and make sure the data that is collected is accurate and pulled out from a relevant source.

A good data analyst course in Gurgaon can be of help! Several data analytics training institutes offer such in-demand skill training course, DexLab Analytics is one of them. For more information, visit their official site.

The blog has been sourced from ― dataconomy.com/2018/10/three-questions-you-need-to-answer-to-succeed-in-data-driven-projects

 

Interested in a career in Data Analyst?

To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.

To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.

Human Element Remains Critical for Enhanced Digital Customer Experience

Posted on by Dexlab

Human Element Remains Critical for Enhanced Digital Customer Experience

Digital customer engagement and service is trending the charts. Companies are found actively focusing on establishing long-lasting relationships in sync with customer expectations to hit better results and profitable outcomes. Customers are even hopeful about businesses implementing smart digital channels to solve complex service issues and finish transactions.

70 % of customers expect companies to have a self-service option in their websites and 50% expect to solve issues concerning products or services themselves – according to Zendesk.

In this regard, below we’ve charted down a few ways to humanize the customer experience, keeping the human aspect in prime focus:

2

Adding Human Element through Brand Stories

Each brand tells a story. But, how, or in what ways do the brands tell their story to the customers? Is it through videos or texts? Brand’s history or values need to be iterated in the right voice to the right audience. Also, the companies must send a strong message saying how well they value their customers and how they always put their customers in the first place, before anything else.

Additionally, the company’s sales team should always look forward to help their customers with after-purchase information – such as how well the customers are enjoying certain features, whether any improvement is needed and more – valuable customer feedback always help at the end of the day!

AI for Feedback

Identify prospective customers who are becoming smarter day by day. This is done via continuous feedback loops along with automated continuous education. Whenever you receive feedback from a specific customer interaction, it’s advised to feed it back to their profile. An enclosed feedback loop is quite important to gain meaningful information about customers and their purchasing pattern. This is the best way to know well your customers and determine what they want and how.

Time and again, customers are asked by brands to take part in specific surveys and rate their services, describing what their feelings are about those particular products or services. All this helps comprehend customer’s satisfaction quotient regarding services, and in a way helps you take necessary action in enhancing customer experience.

Personalized Content for Customer Satisfaction

Keeping customers interested in your content is the key. Become a better story-teller and enhance customer satisfaction. Customers like it when you tell your brand’s story in your own, innovative way. But, of course, marketers face a real challenge when writing down an entertaining story, not appearing like written by agency but themselves.

A token of advice from our side – never go too rigid; be original, and try to narrate the story in an interactive way. To craft a unique brand story, the essence lies in using little wit, humor and a dash of self-effacement to add a beat to the brand.

End Notes

As parting thoughts, we would like to say always act in real-time, and better understand what your customers what and their behavioral traits. This way it would be easier to predict their next move. What’s more, your brand should be people-based and make intelligent use of customer’s available data to develop a deeper understating about your users and their respective needs.

DexLab Analytics is a prime data analyst training institute in Delhi – their data analyst training courses is as per industry standards and brimmed with practical expertise merged with theoretical knowledge. Visit the website now.

 
The blog has been sourced from — dataconomy.com/2018/08/how-to-keep-the-human-element-in-digital-customer-experience
 

Interested in a career in Data Analyst?

To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.

To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.

5 Incredible Techniques to Lift Data Analysis to the Next Level

Posted on by Dexlab

5 Incredible Techniques to Lift Data Analysis to the Next Level

Today, it’s all about converting data into actionable insights. How much data an organization collects from a plethora of sources is all companies cares of. To understand the intricacies of the business operations and helps team identify future trends, data is the power.

Interestingly, there’s more than one way to analyze data. Depending on your requirement and types of data you need to have, the perfect tool for data analytics will fluctuate. Here, we’ve 5 methods of data analysis that will help you develop more relevant and actionable insights.

DexLab Analytics is a premier data analytics training institute in Noida. It offers cutting edge data analyst courses for data enthusiasts.

2

Difference between Quantitative and Qualitative Data:

What type of data do you have? Quantitative or qualitative? From the name itself you can guess quantitative deal is all about numbers and quantities. The data includes sales numbers, marketing data, including payroll data, revenues and click-through rates, and any form of data that can be counted objectively.

Qualitative data is relatively difficult to pin down; they tend to be more subjective and explanatory. Customer surveys, interview results of employees and data that are more inclined towards quality than quantity are some of the best examples of qualitative data. As a result, the method of analysis is less structured and simple as compared to quantitative techniques.

Measuring Techniques for Quantitative Data:

Regression Analysis

When it comes to making forecasts and predictions and future trend analysis, regression studies are the best bet. The tool of regression measures the relationship between a dependent variable and an independent variable.

Hypothesis Testing

Widely known as ‘T Testing’, this type of analytics method boosts easy comparison of data against the hypothesis and assumptions you’ve made regarding a set of operations. It also allows you to forecast future decisions that might affect your organization.

Monte Carlo Simulation

Touted as one of the most popular techniques to determine the impact of unpredictable variables on a particular factor, Monte Carlo simulations implement probability modeling for smooth prediction of risk and uncertainty. This type of simulation uses random numbers and data to exhibit a series of possible outcomes for any circumstance based on any results. Finance, engineering, logistics and project management are a few industries where this incredible tool is widely used.

Measuring Techniques for Qualitative Data:

Unlike quantitative data, qualitative data analysis calls for more subjective approaches, away from pure statistical analysis and methodologies. Though, you still will be able to extract meaningful information from data by employing different data analysis techniques, subject to your demands.

Here, we’ve two such techniques that focus on qualitative data:

Content Analysis

It works best when working with data, like interview data, user feedback, survey results and more – content analysis is all about deciphering overall themes emerging out of a qualitative data. It helps in parsing textual data to discover common threads focusing on improvement.

Narrative Analysis

Narrative analysis help you understand organizational culture by the way ideas and narratives are communicated within an organization. It works best when planning new marketing campaigns and mulling over changes within corporate culture – it includes what customers think about an organization, how employees feel about their job remuneration and how business operations are perceived.

Agreed or not, there’s no gold standard for data analysis or the best way to perform it. You have to select the method, which you deem fit for your data and requirements, and unravel improved insights and optimize organizational goals.

 
The blog has been sourced from — www.sisense.com/blog/5-techniques-take-data-analysis-another-level
 

Interested in a career in Data Analyst?

To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.

To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.

Call us to know more

Gurgaon

+91 8676079880

Kolkata

+91 9903662244

Quick Links

Our Courses

Important dates

Copyright © 2024 DexLab Solutions Corporation | Privacy Policy | Legal Disclaimer | Terms and Conditions