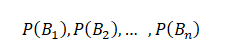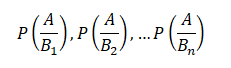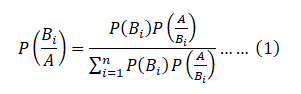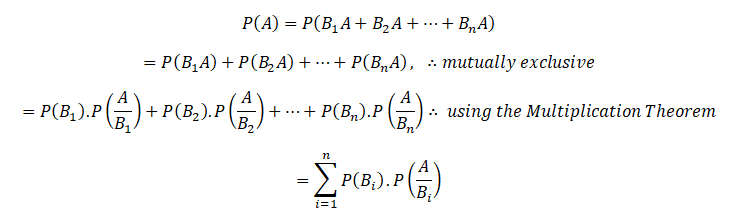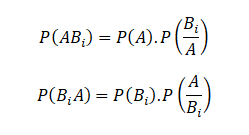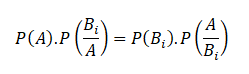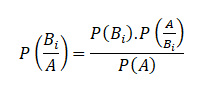Bayes’ theorem, named after 18th century (1763) British mathematician Thomas Bayes, is a mathematical formula for determining conditional probability. In the discussion of conditional probability we indicated that revising probability when new information is obtained is an important phase of probability analysis. Often, we begin our analysis with initial or prior probability estimates for specific events of interest. Then, from sources such as a sample, a special report, a product test, etc we obtain some additional information about the events. Given this new information, we update the prior probability values by calculating revised probabilities, referred to as posterior probabilities.
The steps involved in this probability revision process are depicted in the digram below:
Theorem:
An event A can occur only if one of the mutually exclusive and exhaustive set of events B1, B2,… ,Bn occurs. Suppose that the unconditional probabilities
And the conditional probabilities
are known. Then the conditional probability ![]() of a specified event Bi, when A is stated to have actually occurred, is given by
of a specified event Bi, when A is stated to have actually occurred, is given by
This is known as Bayes’ Theorem.
Proof:
An event A can happen in mutually exclusive ways, B1 A, B2A,… Bn A, i.e. either when has occurred, or. So by the theorem of total probability
Again,
Since the events ABi and BiA are equivalent, their probabilities are also equal.
Hence
So that
Substituting for P(A) from above, the theorem is proved.
Equation (1) is also known as “Bayes” formula for calculating probabilities of hypothesis. Because B1, B2,…Bn may be considered as hypothesis which account for the occurrence of A. The probabilities P(B1),P(B2 ),…P(Bn) are called ‘a prior’ probabilities of the hypothesis.
While ![]() are known as a‘a posteriori’ probabilities of the same hypothesis.
are known as a‘a posteriori’ probabilities of the same hypothesis.

For more on this, do peruse the Dexlab Analytics website today. Dexlab Analytics is a premiere institute for R programming courses in Gurgaon.
.