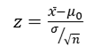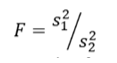In this fifth part of the basic of statistical inference series you will learn about different types of Parametric tests. Parametric statistical test basically is concerned with making assumption regarding the population parameters and the distributions the data comes from. In this particular segment the discussion would focus on explaining different kinds of parametric tests. You can find the 4th part of the series here.
INTRODUCTION
Parametric statistics are the most common type of inferential statistics. Inferential statistics are calculated with the purpose of generalizing the findings of a sample to the population it represents, and they can be classified as either parametric or non-parametric. Parametric tests make assumptions about the parameters of a population, whereas nonparametric tests do not include such assumptions or include fewer. For instance, parametric tests assume that the sample has been randomly selected from the population it represents and that the distribution of data in the population has a known underlying distribution. The most common distribution assumption is that the distribution is normal. Other distributions include the binomial distribution (logistic regression) and the Poisson distribution (Poisson regression).
PARAMETRIC TEST
A parameter in statistics refers to an aspect of a population, as opposed to a statistic, which refers to an aspect, about a sample. For example, the population mean is a parameter, while the sample mean is a statistic. A parametric statistical test makes an assumption about the population parameters and the distributions that the data comes from. These types of tests assume to data is from normal distribution.
Data that is assumed to have been drawn from a particular distribution, and that is used in a parametric test.
Parametric equations are used in calculus to deal with the problems that arise when trying to find functions that describe curves. These equations are beyond the scope of this site, but you can find an excellent rundown of how to use these types of equations here.
The parametric tests are:
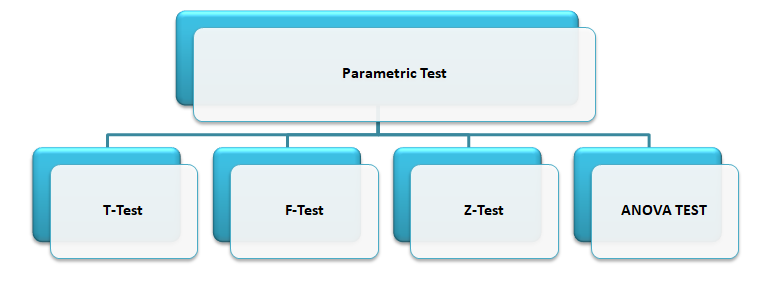 Let’s discuss about each test in details.
Let’s discuss about each test in details.
T-TEST
The T-test is one of, inferential statistics. It is used to determine whether there is a significant difference between the means of two groups or not. When the difference between two population averages is being investigated, a t-test is used. In other words, a t-test is used when we wish to compare two means. Essentially, a t-test allows us to compare the average values of the two data sets and determine if they came from the same population. In the above examples, if we were to take a sample of students from class A and another sample of students from class B, we would not expect them to have exactly the same mean and standard deviation.
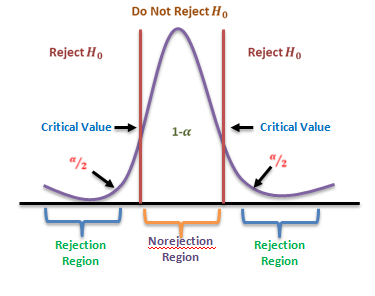
Mathematically, the t-test takes a sample from each of the two sets and establishes the problem statement by assuming a null hypothesis that the two means are equal. Based on the applicable formulas, certain values are calculated and compared against the standard values, and the assumed null hypothesis is accepted or rejected accordingly.
If the null hypothesis qualifies to be rejected, it indicates that data readings are strong and are probably not due to chance. The t-test is just one of many tests used for this purpose. Statisticians must additionally use tests other than the t-test to examine more variables and tests with larger sample sizes. For a large sample size, statisticians use a z-test. Other testing options include the chi-square test and the f-test.
T-Test Assumptions
- The first assumption made regarding t-tests concerns the scale of measurement. The assumption for a t-test is that the scale of measurement applied to the data collected follows a continuous or ordinal scale, such as the scores for an IQ test.
- The second assumption made is that of a simple random sample, that the data is collected from a representative, randomly selected portion of the total population.
- The third assumption is the data, when plotted, results in a normal distribution, bell-shaped distribution curve.
- The final assumption is the homogeneity of variance. Homogeneous, or equal, variance exists when the standard deviations of samples are approximately equal.
There are three types to T-test: (i) Correlated or paired T-test, (ii) Equal variance(or pooled) T-test (iii) Unequal variance T-test.
Z-TEST
A z-test is a statistical test used to determine whether two population means are different when the variances are known and the sample size is large. The test statistic is assumed to have a normal distribution, and nuisance parameters such as standard deviation should be known in order for an accurate z-test to be performed. A z-statistic, or z-score, is a number representing how many standard deviations above or below the mean population a score derived from a z-test is.
The z-test is also a hypothesis test in which the z-statistic follows a normal distribution. The z-test is best used for greater-than-30 samples because, under the central limit theorem, as the number of samples gets larger, the samples are considered to be approximately normally distributed. When conducting a z-test, the null and alternative hypotheses, alpha and z-score should be stated. Next, the test statistic should be calculated, and the results and conclusion stated. Examples of tests that can be conducted as z-tests include a one-sample location test, a two-sample location test, a paired difference test, and a maximum likelihood estimate. Z-tests are closely related to t-tests, but t-tests are best performed when an experiment has a small sample size. Also, t-tests assume the standard deviation is unknown, while z-tests assume it is known. If the standard deviation of the population is unknown, the assumption of the sample variance equaling the population variance is made.
One Sample Z-test: A one sample z test is one of the most basic types of hypothesis test. In order to run a one sample z test, its work through several steps:
Step 1: Null hypothesis is one of the common stumbling blocks–in order to make sense of your sample and have the one sample z test give you the right information it must make sure written the null hypothesis and alternate hypothesis correctly. For example, you might be asked to test the hypothesis that the mean weight gain of an women was more than 30 pounds. Your null hypothesis would be: H0 : μ = 30 and your alternate hypothesis would be H, sub>1: μ > 30.
Step 2: Use the z-formula to find a z-score
All you do is put in the values you are given into the formula. Your question should give you the sample mean (x̄), the standard deviation (σ), and the number of items in the sample (n). Your hypothesized mean (in other words, the mean you are testing the hypothesis for, or your null hypothesis) is μ0 .
Two Sample Z Test: The z-Test: Two- Sample for Means tool runs a two sample z-Test means with known variances to test the null hypothesis that there is no difference between the means of two independent populations. This tool can be used to run a one-sided or two-sided test z-test.
ANOVA
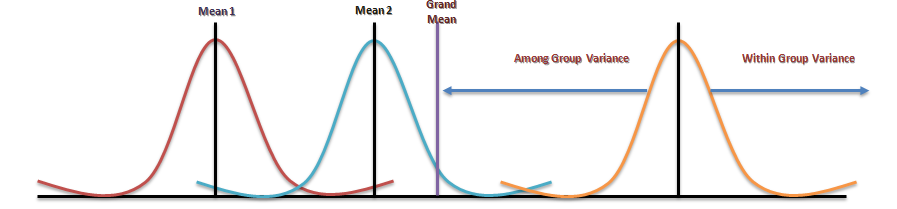
Analysis of variance (ANOVA) is an analysis tool used in statistics that splits an observed aggregate variability found inside a data set into two parts: systematic factors and random factors. The systematic factors have a statistical influence on the given data set, while the random factors do not. Analysts use the ANOVA test to determine the influence that independent variables have on the dependent variable in a regression study.
The ANOVA test is the initial step in analysing factors that affect a given data set. Once the test is finished, an analyst performs additional testing on the methodical factors that measurably contribute to the data set’s inconsistency. The analyst utilizes the ANOVA test results in an f-test to generate additional data that aligns with the proposed regression models. The ANOVA test allows a comparison of more than two groups at the same time to determine whether a relationship exists between them. The result of the ANOVA formula, the F statistic (also called the F-ratio), allows for the analysis of multiple groups of data to determine the variability between samples and within samples.
If no real difference exists between the tested groups, which is called the null hypothesis, the result of the ANOVA’s F-ratio statistic will be close to 1. Fluctuations in its sampling will likely follow the Fisher F distribution. This is actually a group of distribution functions, with two characteristic numbers, called the numerator degrees of freedom and the denominator degrees of freedom.
One-way Anova: A one-way ANOVA uses one independent variable, use a one-way ANOVA when collected data about one categorical independent variable and one quantitative dependent variable. The independent variable should have at least three levels (i.e. at least three different groups or categories). ANOVA that if the dependent variable changes according to the level of the independent variable.
Two-way Anova: A two-way ANOVA is used to estimate how the mean of a quantitative variable changes according to the levels of two categorical variables. Use a two-way ANOVA when you want to know how two independent variables, in combination, affect a dependent variable.
F-TEST
An “F Test” is a catch-all term for any test that uses the F-distribution. In most cases, when people talk about the F-Test, what they are actually talking about is The F-Test to compare two variances. However, the f-statistic is used in a variety of tests including regression analysis, the Chow test and the Scheffe Test (a post-hoc ANOVA test).
F Test to Compare Two Variances
A Statistical F Test uses an F Statistic to compare two variances, s1 and s2 , by dividing them. The result is always a positive number (because variances are always positive). The equation for comparing two variances with the f-test is:
If the variances are equal, the ratio of the variances will equal 1. For example, if you had two data sets with a sample 1 (variance of 10) and a sample 2 (variance of 10), the ratio would be 10/10 = 1.
You always test that the population variances are equal when running an F Test. In other words, you always assume that the variances are equal to 1. Therefore, your null hypothesis will always be that the variances are equal.
Assumptions
Several assumptions are made for the test. Your population must be approximately normally distributed (i.e. fit the shape of a bell curve) in order to use the test. Plus, the samples must be independent events. In addition, you’ll want to bear in mind a few important points:
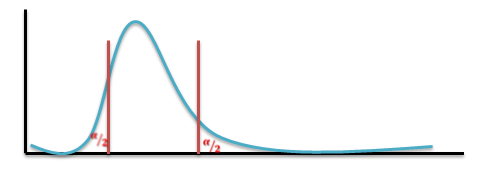
- The larger variance should always go in the numerator (the top number) to force the test into a right-tailed test. Right-tailed tests are easier to calculate.
- For two-tailed tests, divide alpha by 2 before finding the right critical value.
- If you are given standard deviations, they must be squared to get the variances.
- If your degrees of freedom aren’t listed in the F Table, use the larger critical value. This helps to avoid the possibility of Type I errors.
CONCLUSION
Conventional statistical procedures may also call parametric tests. In every parametric test, for example, you have to use statistics to estimate the parameter of the population. Because of such estimation, you have to follow a process that includes a sample as well as a sampling distribution and a population along with certain parametric assumptions that required, which makes sure that all components compatible with one another.
An example can use to explain this. Observations are first of all quite independent, the sample data doesn’t have any normal distributions and the scores in the different groups have some homogeneous variances. Parametric tests are based on the distribution, parametric statistical tests are only applicable to the variables. There’re no parametric tests that exist for the nominal scale date, and finally, they are quite powerful when they exist. There are mainly four types of Parametric Hypothesis Test which already mentioned in previous slides.
Advantages of Parametric Test
One of the biggest and best advantages of using parametric tests is first of all that you don’t need much data that could be converted in some order or format of ranks. The process of conversion is something that appears in rank format and to be able to use a parametric test regularly, you will end up with a severe loss in precision. Another big advantage of using parametric tests is the fact that you can calculate everything so easily. In short, you will be able to find software much quicker so that you can calculate them fast and quick. Apart from parametric tests, there are other non-parametric tests, where the distributors are quite different and they are not all that easy when it comes to testing such questions that focus related to the means and shapes of such distributions.
Disadvantages of Parametric Test
Parametric tests are not valid when it comes to small data sets. The requirement that the populations are not still valid on the small sets of data, the requirement that the populations which are under study have the same kind of variance and the need for such variables are being tested and have been measured at the same scale of intervals. Another disadvantage of parametric tests is that the size of the sample is always very big, something you will not find among non-parametric tests. That makes it a little difficult to carry out the whole test.
This particular discussion on parametric tests ends here, and at the end of this you must have developed clear ideas regarding these test categories. To find more such posts on Data Science training topics follow the Dexlab Analytics blog.
.
Business analysis training, business analytics, business analytics certification, business analytics course in delhi, Business Analytics Online, Uncategorized