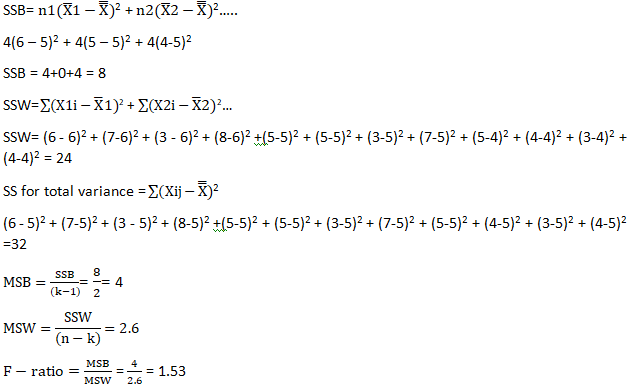In this blog, we are going to be discussing a statistical technique, ANOVA, which is used for comparison.
The basic principal of ANOVA is to test for differences among the mean of different samples. It examines the amount of variation within each of these samples and the amount of variation between the samples. ANOVA is important in the context of all those situations where we want to compare more than two samples as in comparing the yield of crop from several variety of seeds etc.
The essence of ANOVA is that the total amount of variation in a set of data is broken in two types:-
- The amount that can be attributed to chance.
- The amount which can be attributed to specified cause.
One-way ANOVA
Under the one-way ANOVA we compare the samples based on a single factor. For example productivity of different variety of seeds.
Stepwise process involved in calculation of one-way ANOVA is as follows:-
- Calculate the mean of each sample X ̅
- Calculate the super mean
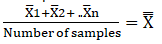
- Calculate the sum of squares between (SSB) samples
- Divide the result by the degree of freedom between the samples to obtain mean square between (MSW) samples.
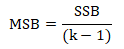
- Now calculate variation within the samples i.e. sum of square within (SSW)
- Calculate mean square within (MSW)
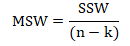
- Calculate the F-ratio
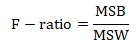
- Last but not the least calculate the total variation in the given samples i.e. sum of square for total variance.
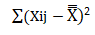
Lets now solve a one-way ANOVA problem.
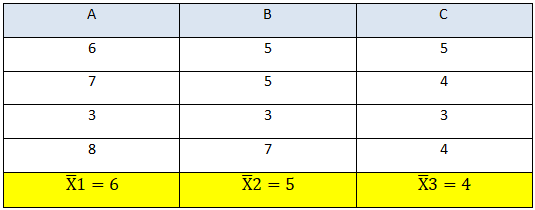
A,B and C are three different variety of seeds and now we need to check if there is any variation in their productivity or not. We will be using one-way ANOVA as there is a single factor comparison involved i.e. variety of seeds.
The f-ratio is 1.53 which lies within the critical value of 4.26 (calculated from the f-distribution table).
Conclusion:- Since the f-ratio lies within the acceptance region we can say that there is no difference in the productivity of the seeds and the little bit of variation that we see is caused by chance.
Two-way ANOVA will be discussed in my next blog so do comeback for the update.
Hopefully, you have found this blog informative, for more clarification watch the video attached down the blog. You can find more such posts on Data Science course topics, just keep on following the DexLab Analytics blog.
.